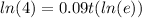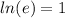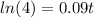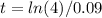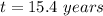Answer:
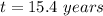
Explanation:
The exponential growth function compounded continuously is equal to
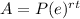
where
A is the final population
P is the initial population
r is the rate of growth in decimal
t is Number of years
e is the mathematical constant number
we have
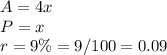
substitute in the function above
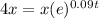
simplify
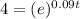
Take natural log of both sides
![ln(4)=ln[(e)^(0.09t)]](https://img.qammunity.org/2020/formulas/mathematics/high-school/lpof42e9f4bxal24ctwfglc3sy06za1m42.png)