Question

Light of wavelength 600 nm in vacuum is incident nearly perpendicularly on a thin film whose index of refraction is 1.5. The light travels from the top surface of the film to the bottom surface, reflects from the bottom surface, and returns to the top surface, as the drawing indicates. What is the total (down-and-back) distance traveled by the light inside the film? Express your answer in terms of the wavelength λfilm of the light within the film.

Answer 1

6λ_film

Step-by-step explanation:

Light of wavelength λ 600 nm

Assuming length of thin film of water to be 1200 nm

Total distance traveled = 2×1200 ×10^{-9} =
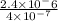`(2.4*10^-6)/(4*10^(-7) )` m

Now, Wavelength of light in film = λ/n

n= refractive index

=
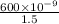`(600*10^(-9))/(1.5)` = 4×10^{-7}

No. of wavelengths = distance traveled/Wavelength of light in film

=
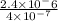`(2.4*10^-6)/(4*10^(-7) )` = 6

therefore, the total (down-and-back) distance traveled by the light inside the film in terms of wavelength λfilm = 6λfilm