Answer:
2 hours
Explanation:
Given: It takes Hank
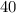 minutes
minutes
 hours to mow a lawn. Penny can mow the same size lawn in
hours to mow a lawn. Penny can mow the same size lawn in
 minutes
minutes
 hours. Hank and Penny form a small lawn care company and have contracts for
hours. Hank and Penny form a small lawn care company and have contracts for
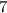 lawns of the same size previously mentioned.
lawns of the same size previously mentioned.
To Find: How long should it take both of them working together to mow the
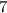 lawns.
lawns.
Solution:
Time taken by Hank to mow the lawn
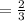
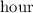
Time taken by Penny to mow the lawn
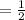
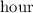
Total lawns to be mowed
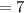
Let time taken by Hank and Penny to mow one lawn
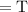
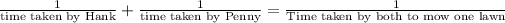
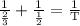
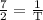
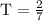
time taken to mow
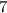 lawns
lawns

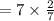
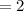
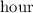
Hence it will take
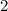
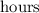 by Hank and Penny to mow
by Hank and Penny to mow
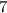 lawns
lawns