Answer:
The rational zero of the polynomial are
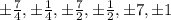 .
.
Explanation:
Given polynomial as :
f(x) = 4 x³ - 8 x² - 19 x - 7
Now the ration zero can be find as
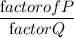 ,
,
where P is the constant term
And Q is the coefficient of the highest polynomial
So, From given polynomial , P = -7 , Q = 4
Now ,
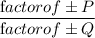
I.e
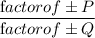 =
=

Or, The rational zero are
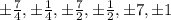
Hence The rational zero of the polynomial are
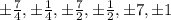 . Answer
. Answer