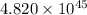Answer:
The number of available energy is
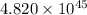
Step-by-step explanation:
Given that,
Energy
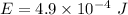
Temperature = 2.7 K
Energy states per unit volume
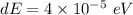
We need to calculate the number of available energy
Using formula of energy
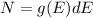
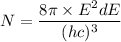
Where, h = Planck constant
c = speed of light
E = energy
Put the value into the formula

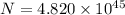
Hence, The number of available energy is