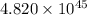Question

The universe is filled with photons left over from the Big Bang that today have an average energy of about 4.9 ✕10-4 (corresponding to a temperature of 2.7 K).

What is the number of available energy states per unit volume for these photons in an interval of 4 ✕10-5eV?

Answer 1

The number of available energy is
`4.820*10^(45)`

Step-by-step explanation:

Given that,

Energy
`E=4.9*10^(-4)\ J`

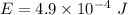
Temperature = 2.7 K

Energy states per unit volume
`dE=4*10^(-5)\ eV`

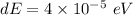
We need to calculate the number of available energy

Using formula of energy

`N=g(E)dE`

`N=(8\pi* E^2 dE)/((hc)^3)`

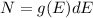
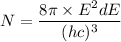
Where, h = Planck constant

c = speed of light

E = energy

Put the value into the formula

`N=(8\pi*(4.9*10^(-4))^2*4*10^(-5)*1.6*10^(-19))/((6.67*10^(-34)*3*10^(8))^3)`

`N=4.820*10^(45)`

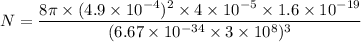
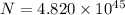
Hence, The number of available energy is
`4.820*10^(45)`