Question

Use the given pair of functions to find and simplify expressions for the following functions and state the domain of each using interval notation.

(g◦f)(x) (f ◦g)(x) (f ◦f)(x)

f(x)= 3−x2, g(x)= (√x+1)

Answer 1

Given functions,

`f(x) = 3 - x^2`

`g(x) = √(x)+1`

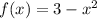
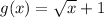
Since, by the compositions of functions,

1. (g◦f)(x) = g(f(x))

`=g(3-x^2)`

`=√(3-x^2)+1`

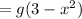
Since, (g◦f) is defined,

If 3 - x² ≥ 0

⇒ 3 ≥ x²

⇒ -√3 ≤ x ≤ √3

Thus, Domain = [-√3, √3]

2. (f◦g)(x) = f(g(x))

`=f(√(x)+1)`

`=3-(√(x)+1)^2`

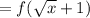
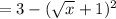
Since, (g◦f) is defined,

If x ≥ 0

Thus, Domain = [0, ∞)

3. (f◦f)(x) = f(f(x))

`=f(3-x^2)`

`=3-(3-x^2)^2`

`=3-9-x^4+6x^2`

`=-6+6x^2-x^4`

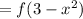
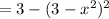
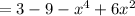
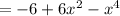
Since, (f◦f) is a polynomial,

We know that,

A polynomial is defined for all real value of x,

Thus, Domain = (-∞, ∞)