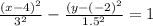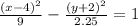Answer:
The equation of the hyperbola in standard form is
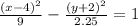
Explanation:
Given:
Centre of the hyperbola=(−2,4)
one vertex of the hyperbola= (−2,7) .
slope of the asymptote = 12
To Find:
The equation of the hyperbola in standard form=?
Solution:
W know that the standard form of hyper bola is
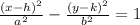 ............................(1)
............................(1)
where
(h,k) is the centre
(x,y) is the vertex of the parabola
a is the length between the centre and the vertices of the hyperbola
b is the distance perpendicular to the transverse axis from the vertex to the asymptotic line
Now the length of a is given by
a=|k-y|
a=|4-7|
a=|-3|
a=3
Also we know that,
Slope =
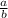 = 2
= 2
=>
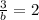
=>
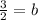
=>b=1.5
Now substituting the known values in equation(1)