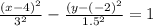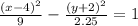Question

The center of a hyperbola is (−2,4) , and one vertex is (−2,7) . The slope of one of the asymptotes is 12 .

What is the equation of the hyperbola in standard form?

Answer 1

`((x+2)^(2))/(1296) - ((y-4)^(2))/(9) = 1`

Explanation:

The standard form of a hyperbola centered at a point distinct from origin has the following form:

`((x-h)^(2))/(a^(2)) - ((y-k)^(2))/(b^(2)) = 1`

The distance between the center and the vertex is:

`b = \sqrt{[(-2)-(-2)]^(2)+(7-4)^(2)}`

`b = 3`

The value of the other semiaxis is:

`(a)/(b) = 12`

`a = 12\cdot b`

`a = 36`

The standard equation of the hyperbola is:

`((x+2)^(2))/(1296) - ((y-4)^(2))/(9) = 1`

Answer 2

The equation of the hyperbola in standard form is
`((x - 4)^2 )/( 9) - ((y +2)^2)/(2.25) = 1`

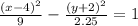
Explanation:

Given:

Centre of the hyperbola=(−2,4)

one vertex of the hyperbola= (−2,7) .

slope of the asymptote = 12

To Find:

The equation of the hyperbola in standard form=?

Solution:

W know that the standard form of hyper bola is

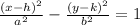`((x - h)^2 )/( a^2) - ((y - k)^2)/(  b^2) = 1`............................(1)

where

(h,k) is the centre

(x,y) is the vertex of the parabola

a is the length between the centre and the vertices of the hyperbola

b is the distance perpendicular to the transverse axis from the vertex to the asymptotic line

Now the length of a is given by

a=|k-y|

a=|4-7|

a=|-3|

a=3

Also we know that,

Slope =
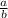`(a)/(b)`= 2

=>
`(3)/(b)=2`

=>
`(3)/(2)=b`

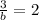
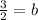
=>b=1.5

Now substituting the known values in equation(1)

`((x - 4)^2 )/( 3^2) - ((y - (-2)^2)/(  1.5^2) = 1`

`((x - 4)^2 )/( 9) - ((y +2)^2)/(2.25) = 1`