Question

3. A satellite is in orbit around some mystery planet. You observe that it takes 3 earth days, or (86,400*3) seconds for this satellite to orbit the mystery planet. a) If the object is located at 7 X 105 meters from this planet, determine the mass of the planet.

Answer 1

3 x 10^18 kg

Step-by-step explanation:

Time period, T = 3 days = 86400 x 3 = 259200 seconds

r = 7 x 10^5 m

Let M be the mass of planet

Use the formula of time period of satellite

`T = 2\pi \sqrt{(r)/(GM)}`

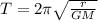
Where, G be the universal gravitational constant.

`M=(4\pi ^(2)r^(3))/(GT^(2))`

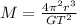
By substituting the values

`M=(4* 3.14 * 3.14* \left ( 7* 10^(5) \right )^(3))/(6.67* 10^(-11)* 259200* 259200)`

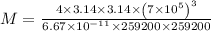
M = 3 x 10^18 kg

Thus , the mass of planet is 3 x 10^18 kg.