Answer:
3 x 10^18 kg
Step-by-step explanation:
Time period, T = 3 days = 86400 x 3 = 259200 seconds
r = 7 x 10^5 m
Let M be the mass of planet
Use the formula of time period of satellite
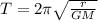
Where, G be the universal gravitational constant.
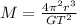
By substituting the values
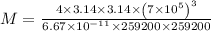
M = 3 x 10^18 kg
Thus , the mass of planet is 3 x 10^18 kg.