Question

On a coordinate plane, parallelogram K L M N shown. Point K is at (7, 7), point L is at (5, 3), point M is at (1, 1), and point N is at (3, 5). Which statement proves that parallelogram KLMN is a rhombus? a. The midpoint of both diagonals is (4, 4). b. The length of KM is
`√(72)` and the length of NL is
`√(8)`. c. The slopes of LM and KN are both One-half and NK = ML =
`√(20)`. d. The slope of KM is 1 and the slope of NL is –1.

Answer 1

Option D.

Explanation:

Given information: KLMN is parallelogram, K(7,7), L(5,3), M(1,1) and N(3,5).

Diagonals of a parallelogram bisect each other.

If diagonals of a parallelogram are perpendicular to each other then the parallelogram is a rhombus.

If a line passes through two points
`(x_1,y_1)` and
`(x_2,y_2)`, then the rate of change is

`m=(y_2-y_1)/(x_2-x_1)`

Slope of KM is

`m_1=(1-7)/(1-7)=1`

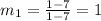
Slope of LN is

`m_2=(5-3)/(3-5)=-1`

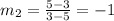
The product of slopes of two perpendicular lines is -1.

Find the product of slopes.

`m_1\cdot m_2=1\cdot (-1)=-1`

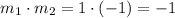
The product of slopes of KM and NL is -1. It means diagonals are perpendicular and KLMN is a rhombus.

Therefore, the correct option is D.