Answer: 0.0047
Explanation:
Given : A manufacturer knows that their items have a normally distributed length, with a mean of 7.1 inches, and standard deviation of 1.7 inches.
i.e.
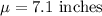
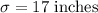
Sample size : n= 24
Let
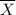 be the sample mean.
be the sample mean.
Formula :
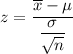
Then, the probability that their mean length is less than 6.2 inches will be :-
![P(\overline{x}<6.2)=P(\frac{\overline{x}-\mu}{(\sigma)/(√(n))}<(6.2-7.1)/((1.7)/(√(24))))\\\\\approx P(z<-2.6)\\\\=1-P(z<2.6)\ \ [\because\ P(Z<-z)=1-P(Z<z)]\\\\=1-0.9953=0.0047\ \ \ [ \text{Using z-value table}]](https://img.qammunity.org/2020/formulas/mathematics/high-school/umpmylmfhp0ibyqaudh31lop8bc5gd3w07.png)
hence,. the required probability = 0.0047