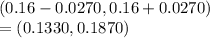Answer:
(0.6728, 0.7672)
(0.1330, 0.1870)
Explanation:
Given that in a recent poll, 600 people were asked if they liked soccer, and 72% said they did.
Std error =
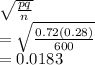
Margin of error for 99% we would use the value
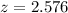
Margin of error =
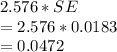
Confidence interval lower bound =
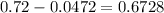
Upper bound =
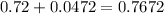
99% confidence interval for the true population proportion of people who like soccer.=(0.6728, 0.7672)
b) n =500
Sample proportion p=
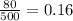
Margin of error for 90% =
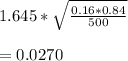
90% confidence interval for the true population proportion of people with kids. =