Question

Does anyone know how to do this and if so can you please help me and explain how to do it, it’ll be appreciated thank you

Answer 1

13)
`(5x)^{-(5)/(4)` ⇒
`\frac{1}{\sqrt[4]{(5x)^5}}`

15)
`(10n)^{(3)/(2)` ⇒
`√((10n)^3)`

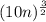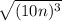
Explanation:

Given expression:

13)
`(5x)^{-(5)/(4)`

15)
`(10n)^{(3)/(2)`

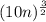
Write the expressions in radical form.

Solution:

For an expression with exponents as fraction like

`(x)^{(m)/(n)`

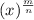
the numerator
`m` represents the power it is raised to and the denominator
`n` represents the nth root of the expression.

For an expression with exponents as negative fraction like

`(x)^{-(m)/(n)`

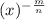
We take the reciprocal of the term by rule for negative exponents.

So it is written as:

`\frac{1}{(x)^{(m)/(n)}}`

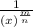
using the above properties we can write the given expressions in radical form.

13)
`(5x)^{-(5)/(4)`

⇒
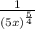`\frac{1}{(5x)^{(5)/(4)}}` [Using rule of negative exponents]

⇒
`\frac{1}{\sqrt[4]{(5x)^5}}` [writing in radical form]

15)
`(10n)^{(3)/(2)`

⇒
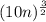
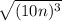`√((10n)^3)` [Since 2nd root is given as
`\sqrt{}` in radical form]