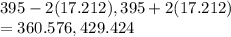Answer:
395, 17.212
(360.576,429.424)
Explanation:
Given that a procedure yields a binomial distribution with n trials and the probability of success for one trial is p.
Here
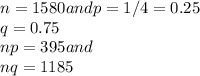
Since np and nq are greater than 5 by rule of thumb we can approximate binomial to normal.
Mean = np = 395
Variance = npq =
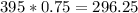
Std dev = 17.212
Thus X no of successes is N(395, 17.212)
THe the minimum usual value mu minus 2 sigma and the maximum usual value mu plus 2 sigma would be