Answer:
C. n=423
Explanation:
1) Notation and important concepts
Margin of error for a proportion is defined as "percentage points your results will differ from the real population value"
Confidence=90%=0.9
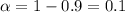 represent the significance level defined as "a measure of the strength of the evidence that must be present in your sample before you will reject the null hypothesis and conclude that the effect is statistically significant".
represent the significance level defined as "a measure of the strength of the evidence that must be present in your sample before you will reject the null hypothesis and conclude that the effect is statistically significant".
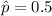 represent the sample proportion of consumers in the Oconee County area who would react favorably to a marketing campaig. For this case since we don't have enough info we use the value of 0.5 since is equiprobable the event analyzed.
represent the sample proportion of consumers in the Oconee County area who would react favorably to a marketing campaig. For this case since we don't have enough info we use the value of 0.5 since is equiprobable the event analyzed.
 represent a quantile of the normal standard distribution that accumulates
represent a quantile of the normal standard distribution that accumulates
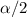 on each tail of the distribution.
on each tail of the distribution.
2) Formulas and solution for the problem
For this case the margin of error for a proportion is given by this formula
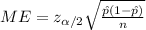 (1)
(1)
For this case the confidence level is 90% or 0.9 so then the significance would be
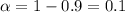 and
and
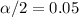
With
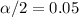 , we can find the value for
, we can find the value for
 using the normal standard distribution table or excel.
using the normal standard distribution table or excel.
The calculated value is
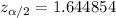
Now from equation (1) we need to solve for n in order to answer the question.

Squaring both sides:
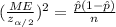
And solving for n we got:
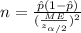
Now we can replpace the values
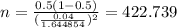
And rounded up to the nearest integer we got:
n=423