Answer:
option E
Step-by-step explanation:
given,
angular speed of bicycle tire ()= 3.80 rad/s
time period = 2.35 s
tire stops and spun in opposite direction with angular velocity = 3.80 rad/s
average angular acceleration
initial angular speed = ω₀ = - 3.80 rad/s
final angular speed = ω₁ = 3.80 rad/s
change in angular velocity
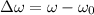
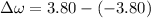
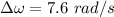
average angular acceleration
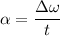

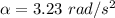
approximately equal to 3.4 rad/s²
the correct answer is option E