Question

Determine algebraically whether the function is even, odd, or neither even nor odd. f(x) = x + 4/x

Answer 1

The given function is an odd function.

Explanation:

We define a function f(x) as even function when f(-x) = f(x) and odd function when f(-x) = - f(x) and otherwise it is neither even nor odd function.

Now, we are given a function of x as
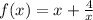`f(x) = x + (4)/(x)` and we have to deternime whether the function f(x) is even, odd, or neither even nor odd.

Now,
`f(-x) = - x + (4)/(- x) = - x - (4)/(x) = - [x + (4)/(x)] = - f(x)`

Therefore, the given function is an odd function. (Answer)