Answer:
16771720740.20324 J
Step-by-step explanation:
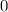 = Density = 0.97 kg/m³
= Density = 0.97 kg/m³
V = Volume =
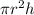
d = Diameter of cylinder = 230 m
r = Radius =
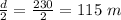
h = Height of the cylinder = 640 m
v = Velocity of cylinder = 51 m/s
Mass of object is given by
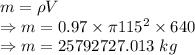
Moment of inertia of a cylinder

Angular speed
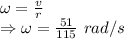
Kinetic energy is given by
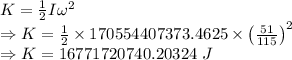
The kinetic energy contained by the tornado is 16771720740.20324 J