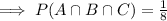Question

A fair coin is tossed three times and the events A, B, and C are defined as follows: A:{ At least one head is observed } B:{ At least two heads are observed } C:{ The number of heads observed is odd } Find the following probabilities by summing the probabilities of the appropriate sample points (note that 0 is an even number):

(a) P(B) =
(b) P(A or B) =
(c) P(A or B or C)

Answer 1

(a) 1/2

(b) 1/2

(c) 1/8

Explanation:

Since, when a fair coin is tossed three times,

The the total number of possible outcomes

n(S) = 2 × 2 × 2

= 8 { HHH, HHT, HTH, THH, HTT, THT, TTH, TTT },

Here, B : { At least two heads are observed } ,

⇒ B = {HHH, HHT, HTH, THH},

⇒ n(B) = 4,

Since,

`\text{Probability}=\frac{\text{Favourable outcomes}}{\text{Total outcomes}}`

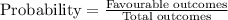
(a) So, the probability of B,

`P(B) =(n(B))/(n(S))=(4)/(8)=(1)/(2)`

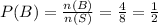
(b) A : { At least one head is observed },

⇒ A = {HHH, HHT, HTH, THH, HTT, THT, TTH},

∵ A ∩ B = {HHH, HHT, HTH, THH},

n(A∩ B) = 4,

`\implies P(A\cap B) = (n(A\cap B))/(n(S)) = (4)/(8)=(1)/(2)`

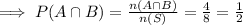
(c) C: { The number of heads observed is odd },

⇒ C = { HHH, HTT, THT, TTH},

∵ A ∩ B ∩ C = {HHH},

⇒ n(A ∩ B ∩ C) = 1,

`\implies P(A\cap B\cap C)=(1)/(8)`