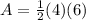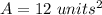Answer:
The area of triangle is 12 square units
Explanation:
we have
The triangle ABC with vertices A(-3,3),B(-3,-3), C(1,-3)
step 1
Using a graphing tool
Plot the triangle
see the attached figure
The triangle ABC is a right triangle
step 2
Find the area of triangle ABC
The area of the triangle ABC is equal to

we have
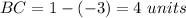 ---> the distance is the difference of the x-coordinates
---> the distance is the difference of the x-coordinates
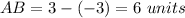 ---> the distance is the difference of the y-coordinates
---> the distance is the difference of the y-coordinates
substitute the values