Question

During a very quick stop, a car decelerates at 7.00 m/s2 . (a) What is the angular acceleration of its 0.280-m-radius tires, assuming they do not slip on the pavement? (b) How many revolutions do the tires make before coming to rest, given their initial angular velocity is 95.0 rad/s ? (c) How long does the car take to stop completely? (d) What distance does the car travel in this time? (e) What was the car’s initial velocity? (f) Do the values obtained seem reasonable, considering that this stop happens very quickly?

Answer 1

-25 rad/s²

29 times

3.8 seconds

50.54 m

26.6 m/s

Step-by-step explanation:

`\omega_f` = Final angular velocity

`\omega_i` = Initial angular velocity

`\alpha` = Angular acceleration

`\theta` = Angle of rotation

a = Acceleration = -7 m/s² (negative because of deceleration)

r = Radius of wheel = 0.28 m

Angular acceleration is given by

`\alpha=(a)/(r)\\\Rightarrow \alpha=(-7)/(0.28)\\\Rightarrow \alpha=-25\ rad/s^`

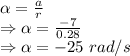
Angular acceleration of the wheel is -25 rad/s²

`\omega_f=\omega_i+\alpha t\\\Rightarrow t=(\omega_f-\omega_i)/(\alpha)\\\Rightarrow t=(0-95)/(-25)\\\Rightarrow t=3.8\ s`

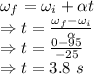
It took 3.8 seconds for the car to stop

`\theta=\omega_it+(1)/(2)\alpha t^2\\\Rightarrow \theta=95* 3.8+(1)/(2)* -25* 3.8^2\\\Rightarrow \theta=180.5\ rad`

`(180.5)/(2\pi)=28.72746\ rev`

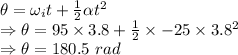
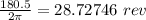
The wheel rotated 29 times.

The

Initial velocity

`u=r\omega_i\\\Rightarrow u=0.28* 95\\\Rightarrow u=26.6\ m/s`

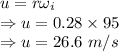
The car’s initial velocity is 26.6 m/s

`s=ut+(1)/(2)at^2\\\Rightarrow s=26.6* 3.8+(1)/(2)* -7* 3.8^2\\\Rightarrow s=50.54\ m`

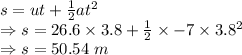
Distance covered in the time is 50.54 m

If the distance is found in meters we get 50.54 m which is very low. Considering the initial velocity is 95.76 km/h. Coming to a stop in that distance is very low. So, the values do not seem reasonable. At least a 100 m is required to stop from that speed.