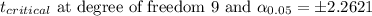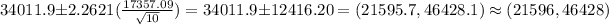Question

A random sample of 10 shipments of stick-on labels showed the following order sizes.10,520 56,910 52,454 17,902 25,914 56,607 21,861 25,039 25,983 46,929PictureClick here for the Excel Data File(a) Construct a 95 percent confidence interval for the true mean order size. (Round your answers to the nearest whole number.) The 95 percent confidence interval to

Answer 1

Confidence Interval: (21596,46428)

Explanation:

We are given the following data set:

10520, 56910, 52454, 17902, 25914, 56607, 21861, 25039, 25983, 46929

Formula:

`\text{Standard Deviation} = \sqrt{\displaystyle\frac{\sum (x_i -\bar{x})^2}{n-1}}`

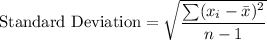
where
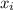`x_i` are data points,
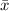`\bar{x}` is the mean and n is the number of observations.

`Mean = \displaystyle\frac{\text{Sum of all observations}}{\text{Total number of observation}}`

`Mean =\displaystyle(340119)/(10) = 34011.9`

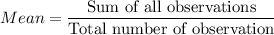
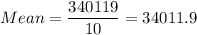
Sum of squares of differences = 551869365.6 + 524322983.6 + 340111052.4 + 259528878 + 65575984.41 + 510538544 + 147644370.8 + 80512934.41 + 64463235.21 + 166851472.4 = 2711418821

`S.D = \sqrt{(2711418821)/(9)} = 17357.09`

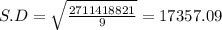
Confidence interval:

`\mu \pm t_(critical)(\sigma)/(√(n))`

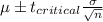
Putting the values, we get,

`t_(critical)\text{ at degree of freedom 9 and}~\alpha_(0.05) = \pm 2.2621`

`34011.9 \pm 2.2621((17357.09)/(√(10)) ) = 34011.9 \pm 12416.20 = (21595.7,46428.1) \approx (21596,46428)`