Answer:
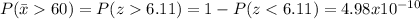
Is a very improbable event.
Explanation:
We want to calculate the probability that the total weight exceeds the limit when the average weight x exceeds 6000/100=60.
If we analyze the situation we this:
If
 represent the 100 random beggage weights for the n=100 passengers . We assume that for each
represent the 100 random beggage weights for the n=100 passengers . We assume that for each
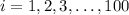 for each
for each
 the distribution assumed is normal with the following parameters
the distribution assumed is normal with the following parameters
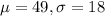 .
.
Another important assumption is that the each one of the random variables are independent.
1) First way to solve the problem
The random variable S who represent the sum of the 100 weight is given by:
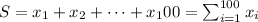
The mean for this random variable is given by:
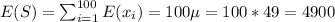
And the variance is given by:
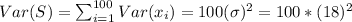
And the deviation:
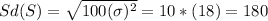
So we have this distribution for S
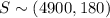
On this case we are working with the total so we can find the probability on this way:
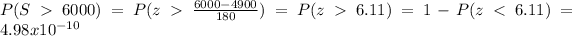
2) Second way to solve the problem
We know that the sample mean have the following distribution:

If we are interested on the probability that the population mean would be higher than 60 we can find this probability like this:
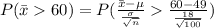
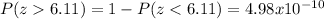
And with both methods we got the same probability. So it's very improbable that the limit would be exceeded for this case.