Question

Railroad tracks are made from segments L = 79 m long at T = 20° C. When the tracks are laid, the engineers leave gaps of width l between adjacent segments to allow for thermal expansion. The coefficient of linear expansion is α = 12 × 10-6 °C-1 and engineers design the tracks to withstand temperatures of Tc = 39.5 degrees.

Answer 1

Step-by-step explanation:

L = 79 m

T1 = 20°C

T2 = 39.5°C

α = 12 x 10^-6/°C

Let the increase in length is ΔL.

According to the linear expansion

ΔL = L x α x ΔT

ΔL = 79 x 12 x 10^-6 x (39.5 - 20)

ΔL = 0.018486 m = 1.8486 cm

The gap between the two rails should be l = 2 x ΔL =

= 2 x 1.8486 = 3.6972 cm

Answer 2

This question is incomplete. This is the complete one:

Railroad tracks are made from segments L = 79 m long at T = 20°C. When the tracks are laid, the engineers leave gaps of width l between adjacent segments to allow for thermal expansion. The coefficient of linear expansion is α = 12 x 10-6 °C-1 and engineers design the tracks to withstand temperatures of TC = 39.5 degrees.

Part (a) Enter an expression, in terms of given variables, for the minimum gap distance l the engineers must leave for a track rated at temperature TC.

Part (b) What is the minimum gap distance in meters?

Part (c) Suppose the engineers forgot to add the gaps at the beginning of 15 segments. How much longer, in meters, would the track be at TC

Step-by-step explanation:

Generally, every solid material has the tendency to expand when it is subjected to heat. This is possible because the kinetic energy and movement of molecules of a substance depend on temperature (K.E =
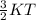`(3)/(2) K T`). As temperature increases, molecules vibrate faster and occupies more space within the material and hence causes it to expand.

part (a)The gap distance, l = αL(Tc - T)

where α is the coefficient of linear expansion, L is the initial length, Tc is the final temperature and T is the initial temperature.

part (b) Linear expansivity α is the increase of a unit length of any material for each degree rise in temperature. Therefore, when the segment is heated to
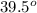`39.5^(o)`C to
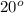`20^(o)`C, there will be rise per unit length for every degree temperature rise. Therefore

l - L =ΔL = αL(Tc - T)

For the two adjacent segments that make up the gap, the minimum gap distance, l = 2αL(Tc - T)

∴ I = 2αL(Tc - T)

= 2 x 12 x 10-6 x 79 x (39.5 - 20)

= 0.036972 m

The minimum gap distance is 0.036972 m

part (c) When 15 segments are involved, the whole length L has increased and become:

L = 15 x 79 = 1185 m.

Therefore, when the gaps are neglected, we have

ΔL = αL(Tc - T)

= 12 x
`10^(-6)` x 1185 x (39.5 - 20)

= 12 x
`10^(-6)` x 1185 x 19.5

= 0.27729 m

The track will be 0.27729 m longer when the gaps are not added.