To solve this problem it is necessary to apply the concepts related to the geometry of a cylindrical tank and its respective definition.
The volume of a tank is given by
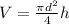
Where
d = Diameter
h = Height
Considering that there are two stages, let's define the initial and final volume as,
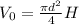
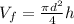
We know as well by definition that
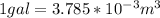
Then we have for the statement that
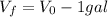
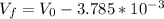
Replacing the previous data


Solving to get h,
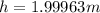
Therefore the change is
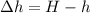
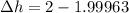

Therefore te change in the height of the water in the tank is 0.37mm