Question

The range of which function is (2, infinity)? y = 2x y = 2(5x) y = 5x +2 y = 5x + 2

Answer 1

y = 5∧× + 2

Explanation:

Answer 2

I think your functions are
`y=2^(x)` ,
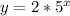`y=2*5^(x)` and
`y=2+5^(x)`

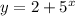
If yes then then the third function which is
`y=2+5^(x)`.

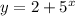Explanation:

The function
`c^(x)` where c is a constant has

Domain :
`c\geq 0`

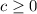
Range : ( 0 , ∞ )

The above range is irrespective of the value of c.

I have attached the graph of each of the function, you can look at it for visualization.

• 
  `y=2^(x)` ⇒ This function is same as
  `c^(x)` so its range is ( 0 , ∞ ).

• 
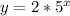  `y=2*5^(x)` ⇒ If we double each value of the function
  `y=5^(x)`, which has range ( 0 , ∞ ), but still the value of extremes won't change as 0*2=0 and ∞*2=∞. Therefore the range remains as ( 0 , ∞ ).

• 
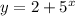  `y=2+5^(x)` ⇒ If we add 2 to each value of the function
  `y=5^(x)`, which has range ( 0 , ∞ ), the lower limit will change as 0+2=2 but the upper limit will be same as ∞. Therefore the range will become as ( 2 , ∞ ).