Answer:
Part A: Section A- 8, Section B- 32.
Part B: 4 times.
Explanation:
The function is given by
 .
.
Section A is from x = 1 to x = 2.
Now, f(1) = 4 × 2 = 8 and f(2) = 4 × 2 × 2 = 16
Again, section B is from x = 3 to x = 4.
Now, f(3) = 4 × 2 × 2 × 2 = 32 and f(4) = 4 × 2 × 2 × 2 × 2 = 64
Part A:
In section A, the average rate of change is =
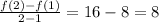 (Answer)
(Answer)
And in section B, the average rate of change is =
 (Answer)
(Answer)
Part B:
Therefore, the number of times the average rate of change of section B is greater than section A is
 (Answer)
(Answer)