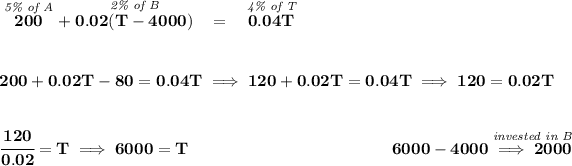Question

$4,000 invested in Fund A returned 5% profit. Amount invested in Fund B returned a 2% profit. How much was invested in Fund B if both funds returned 4%?

Answer 1

as I read it, what I get is that

x = returned profits or yielded interest from investment in A

y = returned profits or yielded interest from investment in B

T = total amount invested or namely A + B.

4000 were invested in A, and it yielded 5%, what's 5% of 4000? (5/100)(4000) = 200 = x.

we know the total amount is T, since A get 4000, B must have gotten T - 4000, or the slack. We also know that B yielded a 2% profit, well, what's 2% of T - 4000? (2/100)(T-4000) = y.

we also know that, whatever "x" and "y" are, their sum total yielded a 4% returns from T, or the total principal, what's 4% of T? (4/100)T = 0.04T.

`\bf \begin{cases} T=\textit{total principal}\\[-0.5em] \hrulefill\\ A=4000\\ x = \stackrel{\textit{5\% of A}}{200}\\[-0.5em] \hrulefill\\ B=T-4000\\ y=\stackrel{\textit{2\% of B}}{0.02(T-4000)} \end{cases} \\\\[-0.35em] ~\dotfill`

`\bf \stackrel{\textit{5\% of A}}{200}+\stackrel{\textit{2\% of B}}{0.02(T-4000)}~~=~~\stackrel{\textit{4\% of T}}{0.04T} \\\\\\ 200+0.02T-80=0.04T\implies 120+0.02T=0.04T\implies 120=0.02T \\\\\\ \cfrac{120}{0.02}=T\implies 6000=T~\hfill \stackrel{~\hfill \textit{invested in B}}{6000-4000\implies 2000}`