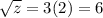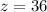Question

The variable x varies directly as the cube of y, and y varies directly as the square root of z. If x equals 1 when z equals 4, what is the value of z when x equals 27?

Answer 1

Answer:B, y=kx^3/square root z

Step-by-step explanation:on edg

Answer 2

`z=36`

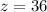
Explanation:

According to the question,

`x`∝
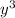`y^3` .......(1)

`y`∝
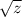`√(z)` .......(2)

From equation 1,2 let constant of proportionality be
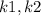`k1,k2` respectively.

⇒
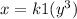`x=k1(y^3)` .......(3)

⇒
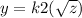`y=k2(√(z) )` .......(4)

From the above equations putting 4 into 3,

`x=k1((k2√(z))^3) =k1.k2^3.(√(z))^3`

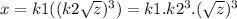
Let the new constant to the above equation be
`k3`,

`x=k3(√(z))^3`

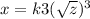
Given,if x=1, when z=4

`1=k3(√(4) )^3=k3(8)`

⇒
`k3=(1)/(8)`

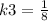
Now if x=27, then z=?

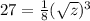
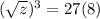
`27=(1)/(8) (√(z) )^3`

⇒
`(√(z) )^3=27(8)`

⇒
`√(z)=3(2)=6`

`z=36`