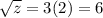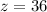Answer:
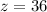
Explanation:
According to the question,
 ∝
∝
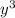 .......(1)
.......(1)
 ∝
∝
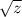 .......(2)
.......(2)
From equation 1,2 let constant of proportionality be
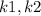 respectively.
respectively.
⇒
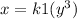 .......(3)
.......(3)
⇒
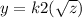 .......(4)
.......(4)
From the above equations putting 4 into 3,
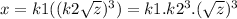
Let the new constant to the above equation be
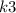 ,
,
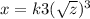
Given,if x=1, when z=4
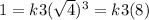
⇒
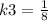
Now if x=27, then z=?
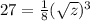
⇒
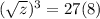
⇒