Question

Can you tell me if they are proportional or nonproportional

Answer 1

4. All of the values are not proportional except 2 values

5. All of the values are non-proportional

6. All of the values are proportional

7. The two variables are proportional when, (no. of pies ordered (one of the variables)) is ≥ 12 . but the two variables are non-proportional when, 0 < (no. of pies ordered (one of the variables)) < 12.

Explanation:

4.All of the values in table 4. are not proportional, except 2 since,

`\frac {1}{17.25} = (4)/(70) \\eq (2)/(35.50)  \\eq (3)/(50.75)`

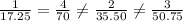
although the units for all fractions is the same i.e., hour/dollar

5. All of the values in table 5 are non-proportional since,

`\frac {1}{37} \\eq \frac {2}{73} \\eq \frac {3}{109} \\eq  (4)/(145)`

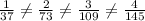
although units for all the fractions are the same. i. e., hour/no. of pages

6. All of the values of the table 6. are proportional, since,

`\frac {1}{2.75} = \frac {2}{5.5} = \frac {3}{8.25} = \frac {4}{11}`

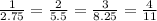
and all of the fractions have same unit i. e., number of lunches/dollar

7. If no, of pies ordered is less than a dozen, then the cost is given by,

y = 5 + 4.5x [y in $, where x is the no. of pies ordered and 0 < x < 12]

clearly, y is not proportional to x.

The table of some values is given by,

x y

1 $ 9.5

2 $ 14

3 $ 18.5 etc.

If no, of pies ordered ≥ 12, then the cost is given by,

m = 4.5n [m in $, where, n is no. of pies ordered and n ≥ 12]

clearly, m is proportional to n

The table of some values is given by,

n m

12 $ 54

13 $ 58.5

14 $ 63 etc.