Question

Use technology or a z-score table to answer the question. Scores on a standardized exam are normally distributed with a mean of 59 and a standard deviation of 8. Consider a group of 5000 students. Approximately how many students will score less than 67 on the exam?

Answer 1

Answer:

C

Step-by-step explanation:

Find P(X > 67)

using ( x - mean )/ standard deviation again you will get thi(1) which is equal to 0.8413....

0.8413 x 5000 is 4207

Explanation:

Answer 2

Approximately 4200 students will score less than 67 on the exam.

Explanation:

Given:

Scores are normally distributed.

Mean score is,
`\mu=59`

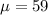
Standard deviation is,
`\sigma=8`

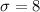
Score is,
`x=67`

Total number of students,
`n=5000`

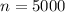
Now, the z score is given as:

`z=(x-\mu)/(\sigma)\\\\z=(67-59)/(8)=(8)/(8)=1`

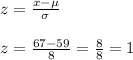
Since, the score is less than 67, therefore, z-score must be less than 1. So,

`z<1`

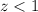
From the z-score table, we observe that for z < 1, the population is 0.8413 or 84.13 % of the total population.

Therefore, the number of students scoring less than 67 is given as:

`Number\ less\ than\ 67\ score=0.8413* 5000=4206.7\approx 4200`

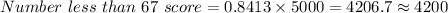
So, approximately 4200 students out of 5000 will get a score less than 67.