Answer:
Approximately 4200 students will score less than 67 on the exam.
Explanation:
Given:
Scores are normally distributed.
Mean score is,
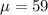
Standard deviation is,
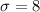
Score is,
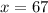
Total number of students,
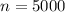
Now, the z score is given as:
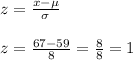
Since, the score is less than 67, therefore, z-score must be less than 1. So,
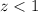
From the z-score table, we observe that for z < 1, the population is 0.8413 or 84.13 % of the total population.
Therefore, the number of students scoring less than 67 is given as:
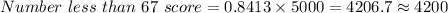
So, approximately 4200 students out of 5000 will get a score less than 67.