Answer:
The probability that their mean length is less than 11.2 inches is 0.5987
Explanation:
Mean = 10.9 inches
Standard deviation = 1.2 inches
We are supposed to find If 25 items are chosen at random, what is the probability that their mean length is less than 11.2 inches
Formula :

We are supposed to find P(x<11.2)

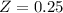
Refer the z table for p value
p value = 0.5987
Hence the probability that their mean length is less than 11.2 inches is 0.5987