Question

Verify The Sum & Difference Identity:

cos(x + y) / sin(x - y) = 1 - cotxcoty / cotx - coty

I’ve struggled with this problem over the last couple of days. Any help is appreciated!

Answer 1

The sum and difference identity cos(x + y) / sin(x - y) = 1 - cotxcoty / cotx - coty is verified

Solution:

Given expression is:

`(\cos (x+y))/(\sin (x-y))=(1-\cot x \cot y)/(\cot x-\cot y)`

Let us first solve L.H.S

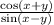`(\cos (x+y))/(\sin (x-y))` ------ EQN 1

We have to use the sum and difference formulas

cos(A + B) = cosAcosB – sinAsinB

sin(A - B) = sinAcosB – cosAsinB

Applying this in eqn 1 we get,

`=(\cos x \cos y-\sin x \sin y)/(\sin x \cos y-\sin y \cos x)`

`\text { Taking sinx } * \text { siny as common }`

`=(\sin x \sin y\left((\cos x \cos y)/(\sin x \sin y)-1\right))/(\sin x \sin y\left((\cos y)/(\sin y)-(\cos x)/(\sin x)\right))`

`\begin{array}{l}{=((\cos x)/(\sin x) * (\cos y)/(\sin y)-1)/((\cos y)/(\sin y)-(\cos x)/(\sin x))} \\\\ {=(\cot x * \cot y-1)/(\cot y-\cot x)} \\\\ {=(\cot x \cot y-1)/(\cot y-\cot x)}\end{array}`

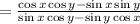
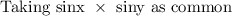
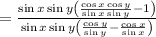
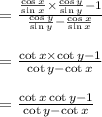
Taking -1 as common from numerator and denominator we get,

`\begin{array}{l}{=(-(1-\cot x \cot y))/(-(\cot x-\cot y))} \\\\ {=((1-\cot x \cot y))/((\cot x-\cot y))}\end{array}`

= R.H.S

Thus L.H.S = R.H.S

Thus the given expression has been verified using sum and difference identity