Question

The equation d=11cos(8pi/5 t) models the horizontal distance, d, in inches of the pendulum of a grandfather clock from the center as it swings from right to left and left to right as a function of time, t, in seconds. According to the model, how long does it take for the pendulum to swing from its rightmost position to its leftmost position and back again? Assume that right of center is a positive distance and left of center is a negative distance. A. 0.625 seconds B. 0.8 seconds C. 1.25 seconds D. 1.6 seconds

Answer 1

Answer: c 1.25

Explanation:

Answer 2

The time it takes for the pendulum to swing from its rightmost position to its leftmost position and back again is 1.25 seconds.

Explanation:

Given the equation

`d = 11cos( (8\pi)/(5)*t)`-----------Equation 1

where d, in inches of the pendulum of a grandfather clock from the center.

Comparing with the standard equation of an oscillating pendulum bob.

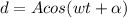`d = Acos (wt + \alpha )` ----------Equation 2

where ω = angular velocity

t = time taken

α = The angular displacement when t = 0

Comparing equation 1 and 2,

α = 0

`w =(8\pi )/(5)`

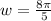
Recall that
`w = 2\pi f</p><p>Therefore,</p><p>[tex]2\pi f = (8\pi )/(5) \\\\f = (4)/(5)`[/tex]

f = 0.8 Hertz

Recall that
`f = (1)/(T)`

`T = (1)/(0.8)`

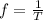
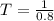
T = 1.25 seconds

Therefore, the time it takes for the pendulum to swing from its rightmost position to its leftmost position and back again is 1.25 seconds.