Question

One way to keep the contents of a garage from becoming too cold on a night when a severe subfreezing temperature is forecast is to put a tub of water in the garage. If the mass of the water is 148 kg and its initial temperature is 22.3°C, how much energy must the water transfer to its surroundings in order to freeze completely?

Answer 1

The energy
`6.311 * 10^(7) \mathrm{J}` is transferred to the surroundings from water in order to freeze completely.

Step-by-step explanation:

Water will transfer to surrounding will come from cooling energy from 22.3°C to 0°C and then freezing energy is

`\mathrm{E}_{\mathrm{t}}=\mathrm{E}_{\text {cooling }}+\mathrm{E}_{\text {freezing }}`

`\mathrm{E}_{\mathrm{t}}=\mathrm{M}\left(\mathrm{C}_{\mathrm{w}} \Delta \mathrm{t}+\mathrm{L}_{\mathrm{f}}\right)`

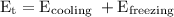
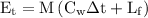
We know that,

\mathrm{C}_{\mathrm{W}}=4190 \mathrm{J} / \mathrm{kgk}

`\mathrm{L}_{\mathrm{f}}=333 * 10^(3) \mathrm{J} / \mathrm{kg}`

As per given question,

M = 148 kg

`\Delta \mathrm{t}=22.3^(\circ) \mathrm{C}`

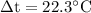
Substitute the values in the above formula,

`\mathrm{E}_{\mathrm{t}}=148\left(4190 * 22.3+333 * 10^(3)\right)`

`E_(t)=148\left(93437+333 * 10^(3)\right)`

`E_(t)=148 * 426437`

`\mathrm{E}_{\mathrm{t}}=6.311 * 10^(7) \mathrm{J}`

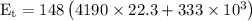
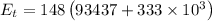
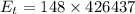
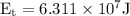
The energy
`6.311 * 10^(7) \mathrm{J}` is transferred to the surroundings from water in order to freeze completely.