The energy
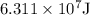 is transferred to the surroundings from water in order to freeze completely.
is transferred to the surroundings from water in order to freeze completely.
Step-by-step explanation:
Water will transfer to surrounding will come from cooling energy from 22.3°C to 0°C and then freezing energy is
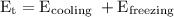
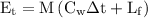
We know that,
\mathrm{C}_{\mathrm{W}}=4190 \mathrm{J} / \mathrm{kgk}
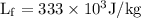
As per given question,
M = 148 kg
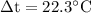
Substitute the values in the above formula,
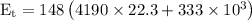
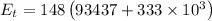
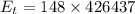
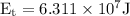
The energy
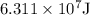 is transferred to the surroundings from water in order to freeze completely.
is transferred to the surroundings from water in order to freeze completely.