Answer:
The point estimate for the population standard deviation of the length of the walking canes is 0.16.
Explanation:
The Central Limit Theorem estabilishes that, for a random variable X, with mean
 and standard deviation
and standard deviation
 , a large sample size can be approximated to a normal distribution with mean
, a large sample size can be approximated to a normal distribution with mean
 and standard deviation
and standard deviation
 .
.
In this problem
The point estimate of the standard deviation is the standard deviation of the sample.
In a sample of 83 walking canes, the average length was found to be 34.9in. with a standard deviation of 1.5. By the Central Limit Theorem, we have that:
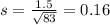
The point estimate for the population standard deviation of the length of the walking canes is 0.16.