Answer:
The value of given expression i.e Ф is 90° and - 30°
Explanation:
Given as :
4 cos²Ф + 2 sinФ = 2
∵ sin²Ф + cos²Ф = 1 , so , cos²Ф = 1 - sin²Ф
Or, 4 ( 1 - sin²Ф ) + 2 sinФ = 2
Or, 4 - 4 sin²Ф + 2 sinФ = 2
or, 4 sin²Ф - 2 sinФ - 4 + 2 = 0
or, 4 sin²Ф - 2 sinФ - 2 = 0
or, 2 sin²Ф - sinФ - 1 = 0
or, 2 sin²Ф - 2 sinФ + sinФ - 1 = 0
Or, 2 sinФ ( sinФ - 1 ) + 1 ( sinФ - 1 ) = 0
∴ ( sinФ - 1 ) ( 2 sinФ + 1 ) = 0
i.e ( sinФ - 1 ) = 0 And ( 2 sinФ + 1 ) = 0
since ( sinФ - 1 ) = 0
So, sinФ = 1
Or, Ф =
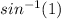 = 90°
= 90°
And ( 2 sinФ + 1 ) = 0
Or, 2 sinФ = - 1
Or, sinФ = -
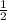
Or, Ф =
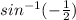 = - 30°
= - 30°
Hence the value of given expression i.e Ф is 90° and - 30° Answer