Question

A rectangle on a coordinate plane has side lengths of 5 units and 4 units, so its diagonal is 41 units. The position of the rectangle is changed by a rigid transformation. What is the length of the diagonal of the transformed rectangle?

Answer 1

Answer: c. 41 units

Explanation:

Answer 2

Length of the diagonal for transformed rectangle is 6.40 units.

Explanation:

A rigid transformation is a translation of the image which has same dimensions.

We know that the “length of the rectangle” = 5 units and the width = 4 units.

The units may be any units of length: inches, cm, feet, miles, km etc.

Calculating “the area of the rectangle”:

Area of this rectangle = length x width (of length x breadth) = 5 × 4= 20 square units

Calculating the perimeter of the rectangle

Perimeter of this rectangle = 2 × (length + width) = 2 × (5+4) = 18 units

Calculating the length of the diagonal of the rectangle

The diagonal of this rectangle may be computed using Pythagorean theorem (or Pythagoras Theorem).

`\text { Length of the diagonals }=\sqrt{\left(5^(2)+4^(2)\right)}`

`\text { Length of the diagonals }=√((25+16))`

`\text { Length of the diagonals }=√(41)`

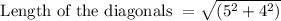
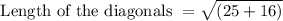
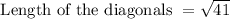
Length of the diagonals = 6.40 units.