Answer:
66.67 ml of 5% solution and 133.33 ml of 6.5% solution are mixed.
Explanation:
Let 200 ml of 6% solution is formed by mixing x ml of 5% solution and y ml of 6.5% solution.
We can write the equation x + y = 200 ........ (1)
Now, x ml of 5% solution will contain
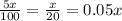 ml of acid
ml of acid
Again, y ml of 6.5% solution will contain
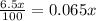 ml of acid.
ml of acid.
So, mixing them together will give (0.05x + 0.065y) ml of acid in 200 ml of solution.
So, from the condition given we can write
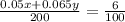
⇒ 0.05x + 0.065y = 12
⇒ x + 1.3 y = 240 ........... (2) {Dividing both sides by 0.05}
Now, solving equations (1) and (2), we get
0.3y = (240 - 200) = 40
⇒ y = 133.33 ml
From equation (1) we get, x = 200 - 133.33 = 66.67 ml
Therefore, 66.67 ml of 5% solution and 133.33 ml of 6.5% solution are mixed. (Answer)