Answer:
The area of given function is 5.67 unit²
Explanation:
Given function f(x) as :
f(x) = 2 x² + 3
The interval in which f(x) lies [ 0 , 2 ]
Let The area for the curve = A
Or , A =
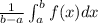
Or, A =

Or, A =
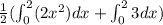
or, A =
![(1)/(2) [2( (2^(3)-0^(3))/(3))] + (1)/(2)[3 (2-0)]](https://img.qammunity.org/2020/formulas/mathematics/high-school/eidf230klho3yq8e1igs4oi66rclznj31r.png)
or, A =
 (
(
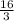 + 6 )
+ 6 )
Or, A =
 ×
×
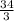
∴ A = 5.67 unit²
Hence The area of given function is 5.67 unit² Answer