Question

A certain company recently sold five-year $1000 bonds with an annual yield of 9.75%. After how much time could they be sold for twice their original price? Give your answer in years and months. (Round your answer to the nearest month.

Answer 1

After 7 years and 5 months.

Explanation:

Let x represent number of years.

We have been given that a certain company recently sold five-year $1000 bonds with an annual yield of 9.75%.

We can see that the value of bond is increasing exponentially, so we will use exponential growth formula to solve our given problem.

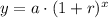`y=a\cdot (1+r)^x`, where,

y = Final value,

a = Initial value,

r = Rate in decimal form,

x = Time

`9.75\%=(9.75)/(100)=0.0975`

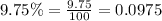
Substituting given values:

`y=1000\cdot (1+0.0975)^x`

`y=1000\cdot (1.0975)^x`

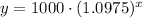
Since we need the selling price to be twice the original price, so we will substitute
`y=2000` in above equation as:

`2000=1000\cdot (1.0975)^x`

`(2000)/(1000)=(1000\cdot (1.0975)^x)/(1000)`

`2=1.0975^x`

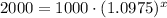
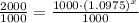
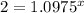
Switch sides:

`1.0975^x=2`

Take natural log of both sides:

`\text{ln}(1.0975^x)=\text{ln}(2)`

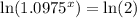
Applying rule
`\text{ln}(a^b)=b\cdot \text{ln}(a)`:

`x\cdot \text{ln}(1.0975)=\text{ln}(2)`

`\frac{x\cdot \text{ln}(1.0975)}{\text{ln}(1.0975)}=\frac{\text{ln}(2)}{\text{ln}(1.0975)}`

`x=(0.6931471805599453)/(0.0930348659671894)`

`x=7.45040231265`

`x\approx 7.4504`

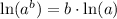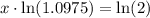
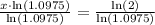
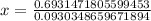
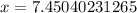
Since x represents time in years, so we need to convert decimal part into months by multiplying .4504 by 12 as 1 year equals 12 months.

7 years and 12*0.4504023 months = 7 years 5.4 months = 7 years 5 months

Therefore, after 7 years and 5 months the company could sold the bonds for twice their original price.