Answer:
The set is a basis for P2
Explanation:
Remember, a set B is a basis for a vector space V if B is a linear independent set and gen(B)=V. Also, remember that the polynomials
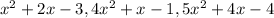 are linearly independent if the unique scalars
are linearly independent if the unique scalars
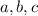 such that
such that
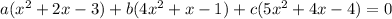
are
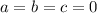
Expanding the above equation we have that
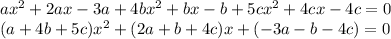
Then we need values of a, b and c such that
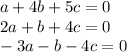
So, we have a homogeneous system with augmented matrix
![A= \left[\begin{array}{ccc}a&4b&5c\\2a&b&4c\\-3a&-b&-4c\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/3ol111hs61m69t7ryhzcu82rioq76t94cy.png)
Now, we apply row operations for solve the system
1. To the second row of A we subtract the first row twice. And to the third row we add the first row three times. We get the matrix:
![\left[\begin{array}{ccc}a&4b&5c\\0&-7b&-6c\\0&11b&11c\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/i9g6h281dn4e5b117vvgmlbc3fuo0xtnnm.png)
2. We multiply the third row of the previous matrix by 1/11
![\left[\begin{array}{ccc}a&4b&5c\\0&-7b&-6c\\0&b&c\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/b4begsui988rk5qrxji7ii8qycpzlnbhje.png)
3. To the third row of the previous matrix we add 7 times the second row.
![\left[\begin{array}{ccc}a&4b&5c\\0&-7b&-6c\\0&0&42c\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/mi9ajv4sz2ioru9siozu6jwxxjuavq3rsm.png)
Since the rank of the matrix is 3 then the system has unique solution. But the system is homogeneous, therefore the solution is
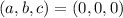
This show that the polynomials are linear independent and therefore the set is a basis for P2