Question

A specimen of a 4340 steel alloy with a plane strain fracture toughness of 54.8 MPa m (50 ksi in. ) is exposed to a stress of 1090 MPa (158100 psi). Assume that the parameter Y has a value of 1.11. (a) If the largest surface crack is 0.8 mm (0.03150 in.) long, determine the critical stress σc.

Answer 1

To solve this problem it is necessary to apply the concepts related to stress failure, stress and last module Young.

Critical stress by definition is given as,

`\sigma_c = (K_(IC))/(Y√(\pi a))`

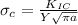
Where,

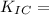`K_(IC) =`Strain fracture toughness

Y = Young's module

a = Length surface crack

Our values are given as,

`K_(IC) = 54.8Mpa`

`Y = 1.11`

`a = 0.8*10^(-3)m`

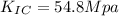
Replacing in our previous equation we have,

`\sigma_c = \frac{54.8}{(1.11)\sqrt{\pi(0.8*10^(-3))}}`

`\sigma_c = 984.77Mpa`

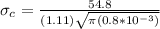
Therefore the critical stress is 984.77Mpa