To solve this problem it is necessary to apply the concepts related to stress failure, stress and last module Young.
Critical stress by definition is given as,
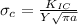
Where,
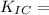 Strain fracture toughness
Strain fracture toughness
Y = Young's module
a = Length surface crack
Our values are given as,
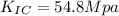
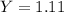

Replacing in our previous equation we have,
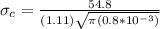
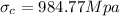
Therefore the critical stress is 984.77Mpa