Answer:
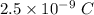
0.00161 A
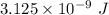
Step-by-step explanation:
C = Capacitance = 1 nF
L = Inductance = 2.4 mH
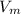 = V = Voltage = 2.5 V
= V = Voltage = 2.5 V
I = Current
Maximum charge in capacitor is given by
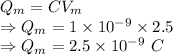
The maximum charge on the capacitor is
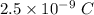
Energy stored in capacitor is given by
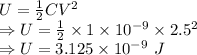
The maximum energy stored in the magnetic field of the coil is
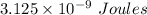
Energy stored in coil is given by
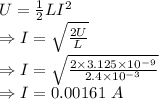
The current passing through the circuit is 0.00161 A